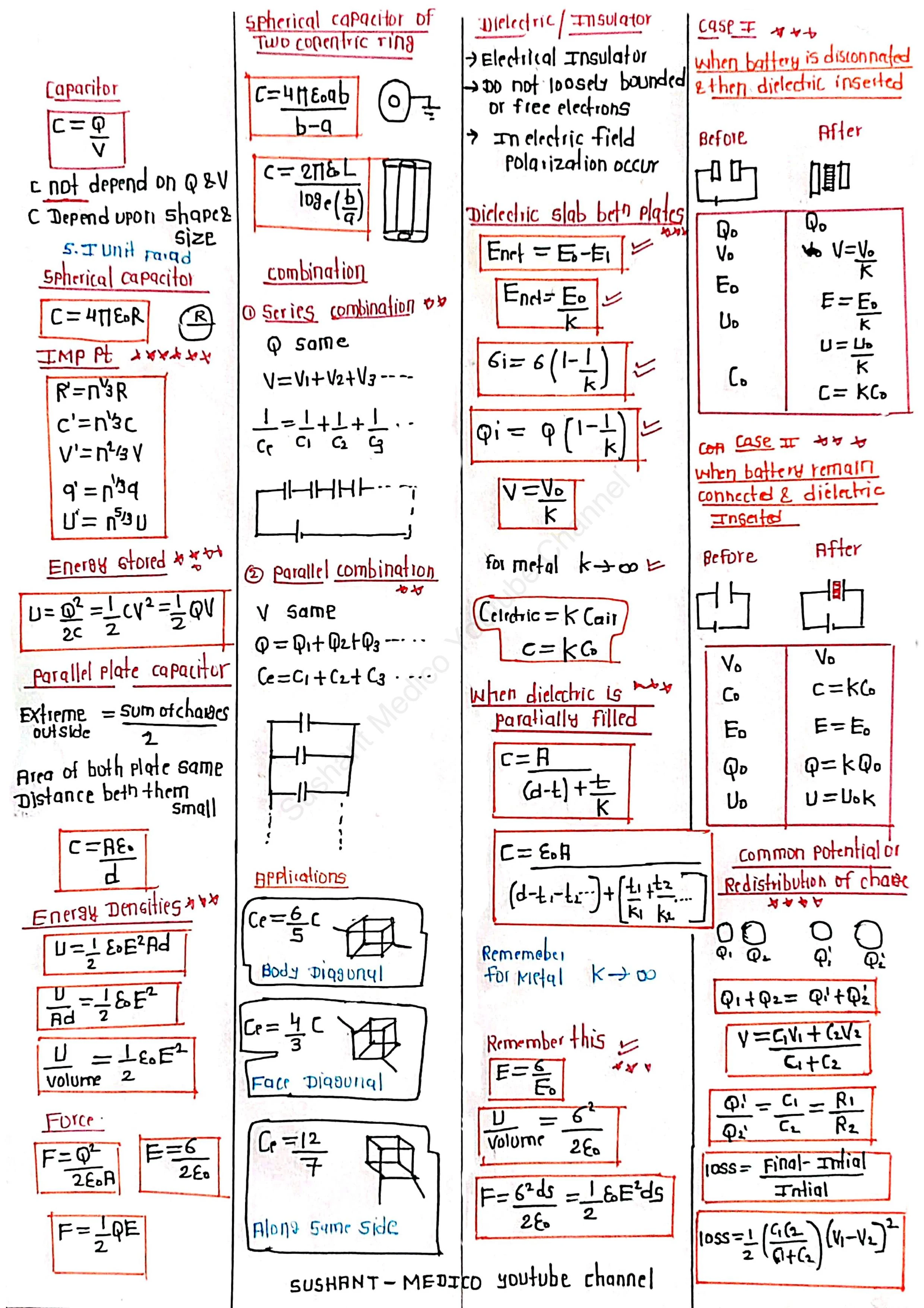
Capacitors - Capacitors are essential components in electrical and electronic circuits, used to store and release electrical energy. They are widely employed in applications ranging from power supply systems to advanced communication technologies. Understanding the concepts of capacitance, energy storage, and the role of dielectrics is key to utilizing capacitors effectively. This article provides a detailed exploration of capacitors, their principles, formulas, and real-world applications.
What is a Capacitor?
A capacitor is a passive electrical component that stores energy in an electric field. It consists of two conductive plates separated by an insulating material known as a dielectric. When a voltage is applied across the plates, an electric field develops, and charge accumulates on the plates, allowing the capacitor to store energy.
Capacitance (C): The Measure of a Capacitor's Ability to Store Charge
The capacitance of a capacitor is defined as the amount of electric charge stored per unit voltage applied across its plates.
Formula:
C = Q / V
Where:
- C = Capacitance (Farads, F)
- Q = Charge stored on the plates (Coulombs, C)
- V = Voltage across the plates (Volts, V)
Key Factors Affecting Capacitance
- Area of the Plates (A): Larger plate area increases capacitance.
- Distance Between Plates (d): Smaller separation increases capacitance.
- Dielectric Material: The type of dielectric determines the permittivity, which directly affects capacitance.
For a parallel plate capacitor:
C = ε₀ × εr × (A / d)
Where:
- ε₀ = Permittivity of free space = 8.85 × 10⁻¹² F/m
- εr = Relative permittivity of the dielectric material
Energy Stored in a Capacitor
A charged capacitor stores energy in the form of an electric field.
Energy Stored (U):
U = ½ × C × V² = ½ × Q × V = Q² / (2 × C)
Capacitor Configurations: Series and Parallel Combinations
1. Capacitors in Series
In a series combination, the total capacitance decreases because the effective plate separation increases.
Formula:
1 / C_total = 1 / C₁ + 1 / C₂ + 1 / C₃ + ...
2. Capacitors in Parallel
In a parallel combination, the total capacitance increases because the effective plate area increases.
Formula:
C_total = C₁ + C₂ + C₃ + ...
Types of Capacitors
Parallel Plate Capacitor:
- Consists of two flat plates separated by a dielectric.
- Capacitance depends on plate area, separation, and dielectric.
Spherical Capacitor:
- Made of two concentric spherical conductors.
- Capacitance: C = 4π × ε₀ × (ab / (b - a)), where a and b are the radii of the inner and outer spheres, respectively.
Cylindrical Capacitor:
- Two concentric cylindrical conductors.
- Capacitance: C = 2πε₀ × (L / ln(b / a)), where L is the length and a, b are the radii.
Dielectrics and Their Role in Capacitors
A dielectric is an insulating material placed between the plates of a capacitor to increase its capacitance. Dielectrics reduce the electric field and increase the ability to store charge by a factor called the dielectric constant (K):
C_with dielectric = K × C_without dielectric
Effect of Dielectrics: Two Cases
When Battery is Disconnected:
- Charge remains constant (Q = constant).
- Capacitance increases (C' = K × C).
- Voltage decreases (V' = V / K).
When Battery Remains Connected:
- Voltage remains constant (V = constant).
- Capacitance increases (C' = K × C).
- Charge increases (Q' = K × Q).
Energy Density of a Capacitor
The energy stored per unit volume in a capacitor is called the energy density.
Formula:
u = ½ × ε × E²
Where:
- u = Energy density (J/m³)
- ε = Permittivity of the dielectric
- E = Electric field strength
Applications of Capacitors
Energy Storage:
- Capacitors store energy for quick discharge, such as in camera flashes and defibrillators.
Filtering:
- Used in electronic circuits to smooth out voltage fluctuations.
Power Supply Systems:
- Capacitors stabilize voltage and reduce noise in power supplies.
Timing Circuits:
- Capacitors are used in combination with resistors to create timing delays.
Tuning Circuits:
- Variable capacitors are used in radio and television tuners to select desired frequencies.
Coupling and Decoupling:
- Coupling capacitors pass AC signals while blocking DC.
- Decoupling capacitors isolate different parts of a circuit.
Common Capacitor Problems and Formulas
Redistribution of Charge
When two capacitors are connected, the charge redistributes, and a common potential is established:
V_common = (C₁V₁ + C₂V₂) / (C₁ + C₂)
Loss of Energy During Redistribution
The energy lost during charge redistribution is:
Energy Loss = ½ × (C₁ × C₂) / (C₁ + C₂) × (V₁ - V₂)²
Key Formulas for Capacitors
| Concept | Formula | Units |
|---|---|---|
| Capacitance | C = Q / V | Farads (F) |
| Parallel Plate Capacitor | C = ε₀ × εr × (A / d) | Farads (F) |
| Energy Stored in Capacitor | U = ½ × C × V² | Joules (J) |
| Capacitors in Series | 1 / C_total = 1 / C₁ + 1 / C₂ | Farads (F) |
| Capacitors in Parallel | C_total = C₁ + C₂ + C₃ | Farads (F) |
| Spherical Capacitor | C = 4πε₀ × (ab / (b - a)) | Farads (F) |
| Energy Density | u = ½ × ε × E² | J/m³ |
| Common Potential | V_common = (C₁V₁ + C₂V₂) / (C₁ + C₂) | Volts (V) |
FAQs
What is the main function of a capacitor?
A capacitor stores electrical energy and releases it when needed. It is used for energy storage, filtering, and voltage stabilization in circuits.How does a dielectric affect a capacitor?
A dielectric increases the capacitance by reducing the electric field strength and allowing more charge to be stored on the plates.What happens when capacitors are connected in series?
The total capacitance decreases because the effective plate separation increases.Why is energy lost during charge redistribution?
Energy is lost as heat due to resistive elements in the circuit during charge redistribution between capacitors.What are real-life examples of capacitors?
Capacitors are used in devices like smartphones, power supplies, televisions, and electric vehicles.How does a parallel plate capacitor work?
A parallel plate capacitor stores charge on its plates when a voltage is applied, creating an electric field in the dielectric between the plates.Capacitors are versatile components that play a critical role in modern technology. By mastering their principles and applications, engineers and scientists can design efficient electronic systems and innovate new technologies.